数据结构

树的遍历

遍历算法分析

遍历和创建树的过程都是递归的（算法思想都是递归的，就算是非递归算法仍然是按照递归思想实现的），只是按照某种遍历方式遍历子树时和访问树的方式一样。

注意子树和结点的区别

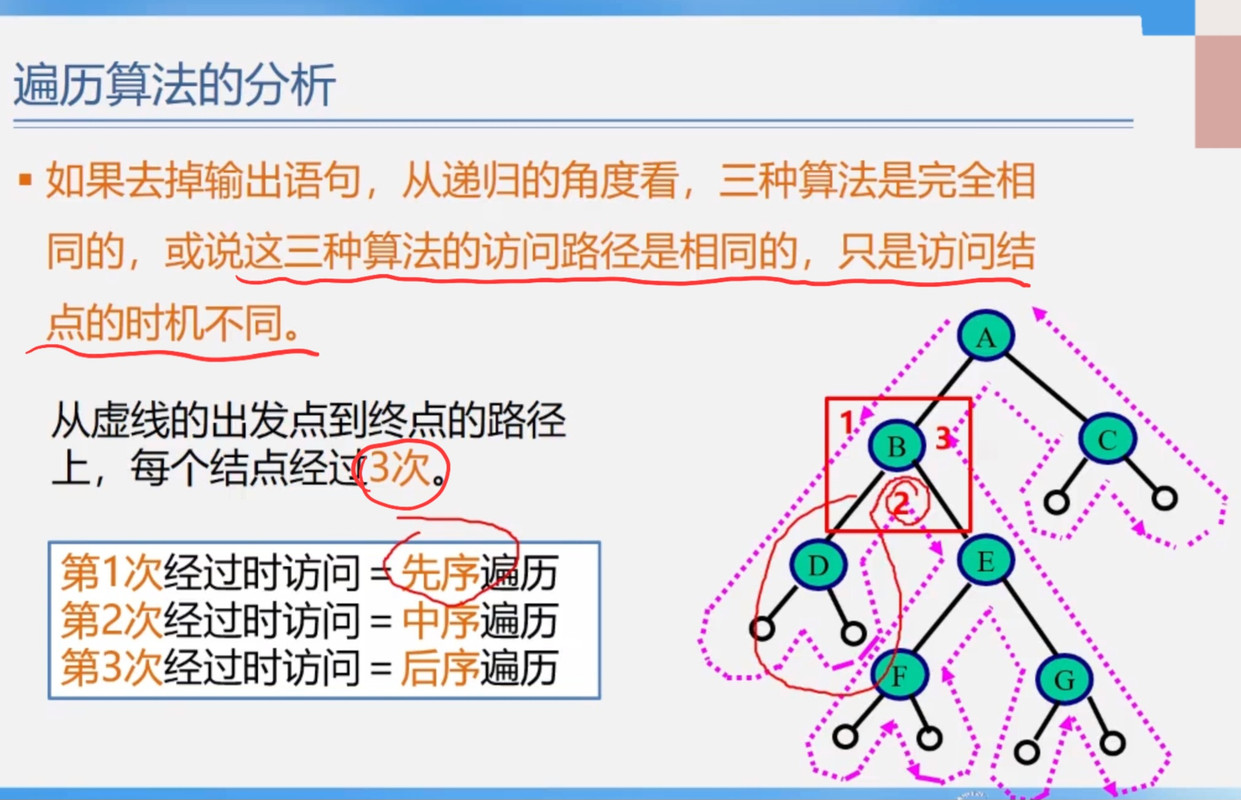
每个节点在递归调用的时候都会经过3次，不同的遍历顺序只是访问的时机不一样。

2024-11-26.jpg

图片来自青岛大学王卓老师的PPT

先序遍历：先访问根节点，先序遍历左子树，先序遍历右子树

先序遍历左子树的时候同样是先访问根节点，再先序遍历左子树的左子树，等到第一颗左子树的所有子孙被访问完之后再先序遍历右子树。

递归算法实现

Status preOrderTraverse(BiTree T) {
    if (T == NULL) {
        return OK;
    } else {
        visit(T);
        preOrderTraverse(T->lchild);
        preOrdreTraverse(T->rchild);
    }
}

递归算法时间复杂度太高，需要先访问完一层之后才能回到上一层

一层一层地发生了多次调用，直到第一次调用的返回主函数，每次调用的参数都是不一样的。

非递归算法实现

// 树节点
typedef struct TreeNode {
    int data;
    struct TreeNode *lchild;
    struct TreeNode *rchild;
} TreeNode, *Tree;

// 栈的实现----------------------------------------------------------------
typedef TreeNode *elemType;

typedef struct Stack {
    elemType *array;
    int top;
    int capacity;
} Stack;

Stack *creatStack(int capacity) {
    Stack *stack = (Stack *)malloc(sizeof(Stack));
    stack->capacity = capacity;
    stack->top = -1;
    stack->array = (elemType *)malloc(capacity * sizeof(elemType));
    return stack;
}

int isEmpty(Stack *stack) {
    return stack->top == -1;
}

int isFull(Stack *stack) {
    return stack->top == stack->capacity - 1;
}

void push(Stack *stack, elemType) {
    if (isFull(stack)) return;
    stack->array[++(stack->top)] = elemType;
}

elemType pop(Stack *stack) {
    if (!isEmpty(stack)) {
        return stack->array[(stack->top)--];
    }
    // 否则返回对应数据类型的空值(自己设定或通用例如 NULL)
    return INT_MAX;
}
// -------------------------------------------------------------------

void inorderTraversal(Tree root) {
    if (root == NULL) return;
    Stack *stack = creatStack(100);
    TreeNode *node = root;
    // 如果非空或者根节点不为空
    while (!isEmpty(stack) || node) {
        // 一直往左下寻找，找到最左孩子
        while (node) {
            push(stack, node);
            node = node->lchild;
        }
        // 栈里存放的没有访问过的节点
        if (!isEmpty(stack)) {
            // pop操作相当于递归中的返回上一层
            node = pop(stack);
            // 访问根节点
            printf("%d", node->data);
            // 访问右子树
            node = node->rchild;
        }
    }
    free(stack);
}

中序遍历：中序遍历左子树，再访问根节点，中序遍历右子树

只是访问时机不一样

todo

后序遍历：后序遍历左子树，后序遍历右子树，再访问根节点

非递归遍历算法可以用栈和队列来实现。

todo

backtop